The binpacking problem consists of the task to distribute a given set of items ![$ [n] := \{1, \dots, n\}$](form_0.png) with nonnegative size
with nonnegative size 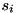 to a minimal number of bins, all of the same capacity
to a minimal number of bins, all of the same capacity 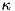 . As example consider 9 items with sizes: 2, 1, 2, 1, 1, 2, 3, 2, and 1 and a bin capacity of
. As example consider 9 items with sizes: 2, 1, 2, 1, 1, 2, 3, 2, and 1 and a bin capacity of 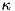 of 4. The following pictures show a feasible solution which needs 5 bins. The minimum number of bins needed for that example is 3.
of 4. The following pictures show a feasible solution which needs 5 bins. The minimum number of bins needed for that example is 3.
This problem can be formulated as a set covering problem as discussed by Gilmore and Gomory in the following two classical papers:
- Gilmore P. C., R. E. Gomory: A linear programming approach to the cutting-stock problem. Operations Research 9 (1961): 849-859.
- Gilmore P. C., R. E. Gomory: A linear programming approach to the cutting-stock problem - Part II. Operations Research 11 (1963): 863-888
We introduce a binary variable 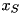 for each feasible packing
for each feasible packing 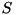 . A packing
. A packing 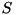 is an assignment vector
is an assignment vector 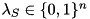 which states the items belonging to that packing. It is feasible, if and only if the total size of the items contained in this assignment is not greater than the given capacity
which states the items belonging to that packing. It is feasible, if and only if the total size of the items contained in this assignment is not greater than the given capacity 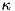 . Let
. Let 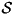 be the set of all feasible packing, this measns:
be the set of all feasible packing, this measns:
![\[ \mathcal{S} := \{S\subseteq [n] \mid \sum_{i:i\in S} s_{i} \leq \kappa \} \]](form_7.png)
An integer program can be formulated as follows:
![\[ \begin{array}[t]{rll} \min & \displaystyle \sum_{S \in \mathcal{S}} x_{S} \\ & \\ subject \ to & \displaystyle \sum_{S \in \mathcal{S}} (\lambda_{S})_{i}x_{S} \ge 1 & \quad \forall i \in \{1,\dots,n\} \\ & \\ & x_{S} \in \{0,1\} & \quad \forall S \in \mathcal{S} \\ \end{array} \]](form_8.png)
This means we are searching for a set of packings such that each item is contained in at least one of the selected packings. Since the objective is to minimize the number of used packings, each optimal solution to the above problem can be transformed into a solution where each item is packed exactly once with the same cost.
Since 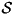 can be of exponential size, we are using a column generation approach to solve this problem. We initialize the (master) problem with a set of
can be of exponential size, we are using a column generation approach to solve this problem. We initialize the (master) problem with a set of 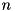 variables representing packings of a single item per bin. Now, we have to iteratively search for variables representing "better" packings, i.e., a packing pattern which reduces the overall cost. For a given solution
variables representing packings of a single item per bin. Now, we have to iteratively search for variables representing "better" packings, i.e., a packing pattern which reduces the overall cost. For a given solution 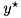 of the (restricted) dual linear program, we have to find a variable/packing
of the (restricted) dual linear program, we have to find a variable/packing 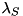 for which the reduced costs is negative. This means:
for which the reduced costs is negative. This means:
![\[ c_{S} - \sum_{i=0}^n (\lambda_S)_i y_i^\star < 0. \]](form_12.png)
Since all variables 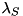 have an objective coefficient
have an objective coefficient 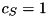 the above condition is equivalent to
the above condition is equivalent to
![\[ \sum_{i=0}^n (\lambda_S)_i y_i^\star > 1. \]](form_14.png)
To find such a variable/packing we solve the following integer program:
![\[ \begin{array}[t]{rll} \max & \displaystyle \sum_{i=1}^n (\lambda_S)_i y^\star_i\\ & \\ subject \ to & \displaystyle \sum_{i=0}^n (\lambda_S)_i s_i \leq \kappa \\ & \\ & (\lambda_S)_i \in \{0,1\} & \quad \forall i \in \{ 1, \dots , n \} \\ \end{array} \]](form_15.png)
where 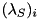 for
for 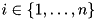 are binary variables and
are binary variables and 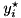 given by the dual solution of the restricted master problem.
given by the dual solution of the restricted master problem.
The above problem is a knapsack problem which can be solved via dynamic programming or by solving the above integer program. In this example we implemented a pricer which solves the integer program.


![$ [n] := \{1, \dots, n\}$](form_0.png) with nonnegative size
with nonnegative size 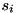 to a minimal number of bins, all of the same capacity
to a minimal number of bins, all of the same capacity 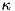 . As example consider 9 items with sizes: 2, 1, 2, 1, 1, 2, 3, 2, and 1 and a bin capacity of
. As example consider 9 items with sizes: 2, 1, 2, 1, 1, 2, 3, 2, and 1 and a bin capacity of 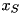 for each feasible packing
for each feasible packing 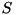 . A packing
. A packing 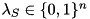 which states the items belonging to that packing. It is feasible, if and only if the total size of the items contained in this assignment is not greater than the given capacity
which states the items belonging to that packing. It is feasible, if and only if the total size of the items contained in this assignment is not greater than the given capacity 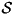 be the set of all feasible packing, this measns:
be the set of all feasible packing, this measns:![\[ \mathcal{S} := \{S\subseteq [n] \mid \sum_{i:i\in S} s_{i} \leq \kappa \} \]](form_7.png)
![\[ \begin{array}[t]{rll} \min & \displaystyle \sum_{S \in \mathcal{S}} x_{S} \\ & \\ subject \ to & \displaystyle \sum_{S \in \mathcal{S}} (\lambda_{S})_{i}x_{S} \ge 1 & \quad \forall i \in \{1,\dots,n\} \\ & \\ & x_{S} \in \{0,1\} & \quad \forall S \in \mathcal{S} \\ \end{array} \]](form_8.png)
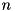 variables representing packings of a single item per bin. Now, we have to iteratively search for variables representing "better" packings, i.e., a packing pattern which reduces the overall cost. For a given solution
variables representing packings of a single item per bin. Now, we have to iteratively search for variables representing "better" packings, i.e., a packing pattern which reduces the overall cost. For a given solution 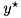 of the (restricted) dual linear program, we have to find a variable/packing
of the (restricted) dual linear program, we have to find a variable/packing 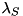 for which the reduced costs is negative. This means:
for which the reduced costs is negative. This means:![\[ c_{S} - \sum_{i=0}^n (\lambda_S)_i y_i^\star < 0. \]](form_12.png)
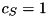 the above condition is equivalent to
the above condition is equivalent to![\[ \sum_{i=0}^n (\lambda_S)_i y_i^\star > 1. \]](form_14.png)
![\[ \begin{array}[t]{rll} \max & \displaystyle \sum_{i=1}^n (\lambda_S)_i y^\star_i\\ & \\ subject \ to & \displaystyle \sum_{i=0}^n (\lambda_S)_i s_i \leq \kappa \\ & \\ & (\lambda_S)_i \in \{0,1\} & \quad \forall i \in \{ 1, \dots , n \} \\ \end{array} \]](form_15.png)
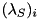 for
for 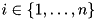 are binary variables and
are binary variables and 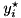 given by the dual solution of the restricted master problem.
given by the dual solution of the restricted master problem.