SCIP
Solving Constraint Integer Programs
Solving Constraint Integer Programs
|
All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Groups Pages
prop_genvbounds.h File Reference Detailed Descriptiongeneralized variable bounds propagator A generalized variable bound is a linear inequality of the form
where
Note that for feasible problems, The genvbounds propagator sorts its stored generalized variable bounds topologically in the following order: A generalized variable bound A ( Both global and local propagation is applied: If the primal bound improves, generalized variable bounds with a nonzero coefficient d are enforced in order to tighten global bounds using the global variable bounds for computing the minactivity. Independently, the genvbounds propagator catches events SCIP_EVENTTYPE_LBTIGHTENED and SCIP_EVENTTYPE_UBTIGHTENED, i.e., locally tightened bounds of variables that occur in the right-hand sides of generalized variable bounds, in order to perform an efficient local propagation when called. Definition in file prop_genvbounds.h. #include "scip/scip.h"Go to the source code of this file.
Function Documentation
adds a generalized variable bound to the genvbounds propagator; if there is already a genvbound for the bound "boundtype" of variable "var", it will be replaced
creates the genvbounds propagator and includes it in SCIP
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\[ c \, x_i \geq \sum (a_j \, x_j) + d \cdot \mbox{primal\_bound} + \mbox{const}, \]](form_150.png)
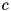is either 1 or -1 and 
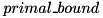is an upper bound on the optimal objective value, which may improve during the solving process. In SCIP, generalized variable bounds are used for providing bounds on the LHS's variable 
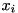. If the above inequality is valid, the following bounds, depending on ![\[ c = 1 \qquad\Rightarrow\qquad x_i \geq \mbox{minactivity}(\sum a_j \, x_j) + d \cdot \mbox{primal\_bound} + \mbox{const} \]](form_152.png)
![\[ c = -1 \qquad\Rightarrow\qquad x_i \leq - \mbox{minactivity}(\sum a_j \, x_j) - d \cdot \mbox{primal\_bound} - \mbox{const}. \]](form_153.png)
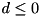must hold. If 
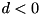a decrease of the primal bound causes an improvement of the provided bound. Similarly, if 
( 
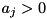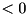), a tightened lower (upper) bound of a variable 
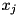also yields a better bound for 
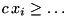) preceeds a generalized variable bound B if the left-hand side variable of A appears in the right-hand side of B with sign of its coefficient equal to c; i.e., if A is propagated and tightens the corresponding bound of x_i, then the minactivity on the right-hand side of B increases. We assume that this order is acyclic for the generalized variable bounds added. Under this condition, propagating the generalized variable bounds in a topological order ensures that all propagations are found in one round.