|
All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Groups Pages
How to add branching rules Branching rules are used to split the problem at the current node into smaller subproblems. Branching rules can be called at three different occasions, which is why they have three different execution methods (see Additional Callback Methods of a Branching Rule). Branching is performed if:
The idea of branching rules is to take a global view on the problem. In contrast, branching paradigms which are specific to one type of constraint are best implemented within the enforcement callbacks of your constraint handler. See, e.g., the constraint specific branching rules provided by the constraint handlers for special ordered sets (src/scip/cons_sos{1,2}.c)). We now explain how users can add their own branching rules. Take the most infeasible LP branching rule (src/scip/branch_mostinf.c) as an example. As all other default plugins, it is written in C. C++ users can easily adapt the code by using the scip::ObjBranchrule wrapper base class and implement the scip_...() virtual methods instead of the SCIP_DECL_BRANCH... callback methods. Additional documentation for the callback methods of a branching rule can be found in the file type_branch.h. Here is what you have to do to implement a branching rule:
Properties of a Branching RuleAt the top of the new file "branch_mybranchingrule.c" you can find the branching rule properties. These are given as compiler defines. In the C++ wrapper class, you have to provide the branching rule properties by calling the constructor of the abstract base class scip::ObjBranchrule from within your constructor. The properties you have to set have the following meaning:
Branching Rule DataBelow the header "Data structures" you can find a struct which is called "struct SCIP_BranchruleData". In this data structure, you can store the data of your branching rule. For example, you should store the adjustable parameters of the branching rule in this data structure. If you are using C++, you can add branching rule data as usual as object variables to your class. Interface MethodsAt the bottom of "branch_mybranchingrule.c", you can find the interface method SCIPincludeBranchruleMybranchingrule(), which also appears in "branch_mybranchingrule.h" SCIPincludeBranchruleMybranchingrule() is called by the user, if (s)he wants to include the branching rule, i.e., if (s)he wants to use the branching rule in his/her application. This method only has to be adjusted slightly. It is responsible for notifying SCIP of the presence of the branching rule. For this, you can either call SCIPincludeBranchrule(), or SCIPincludeBranchruleBasic() since SCIP version 3.0. In the latter variant, additional callbacks must be added via setter functions as, e.g., SCIPsetBranchruleCopy(). We recommend this latter variant because it is more stable towards future SCIP versions which might have more callbacks, whereas source code using the first variant must be manually adjusted with every SCIP release containing new callbacks for branchrule in order to compile. If you are using branching rule data, you have to allocate the memory for the data at this point. You can do this by calling: SCIP_CALL( SCIPallocMemory(scip, &branchruledata) );
You also have to initialize the fields in struct SCIP_BranchruleData afterwards. You may also add user parameters for your branching rule, see the method SCIPincludeBranchruleRelpscost() in src/scip/branch_relpscost.c for an example. Fundamental Callback Methods of a Branching RuleBranching rules do not have any fundamental callback methods, i.e., all callback methods are optional. In most cases, however, you want to implement the BRANCHEXECLP method and sometimes the BRANCHEXECPS method. Additional Callback Methods of a Branching RuleThe additional callback methods do not need to be implemented in every case. However, some of them have to be implemented for most applications, they can be used, for example, to initialize and free private data. Additional callbacks can either be passed directly with SCIPincludeBranchrule() to SCIP or via specific setter functions after a call of SCIPincludeBranchruleBasic(), see also Interface Methods. The most important callback methods are the BRANCHEXECLP, BRANCHEXECEXT, and BRANCHEXECPS methods, which perform the actual task of generating a branching. Additional documentation for the callback methods can be found in type_branch.h. BRANCHEXECLPThe BRANCHEXECLP callback is executed during node processing if a fractional LP solution is available. It should split the current problem into smaller subproblems. Usually, the branching is done in a way such that the current fractional LP solution is no longer feasible in the relaxation of the subproblems. It is, however, possible to create a child node for which the fractional LP solution is still feasible in the relaxation, for example, by branching on a variable with integral LP value. In every case, you have to make sure that each subproblem is a proper restriction of the current problem. Otherwise, you risk to produce an infinite path in the search tree. The user gains access to the branching candidates, i.e., to the fractional variables, and their LP solution values by calling the method SCIPgetLPBranchCands(). Furthermore, SCIP provides two methods for performing the actual branching, namely SCIPbranchVar() and SCIPcreateChild(). Given an integral variable Please also see the further information for the three execution methods. BRANCHEXECEXTThe BRANCHEXECEXT callback is executed during node processing if no LP solution is available and the list of external branching candidates is not empty. It should split the current problem into smaller subproblems. If you do not use relaxation handlers or constraints handlers that provide external branching candidates, you do not need to implement this callback. In contrast to the LP branching candidates and the pseudo branching candidates, the list of external branching candidates will not be generated automatically. The user has to add all variables to the list by calling SCIPaddExternBranchCand() for each of them. Usually, this will happen in the execution method of a relaxation handler or in the enforcement methods of a constraint handler. The user gains access to these branching candidates by calling the method SCIPgetExternBranchCands(). Furthermore, SCIP provides two methods for performing the actual branching with a given solution value, namely SCIPbranchVarVal() and SCIPcreateChild(). SCIPbranchVarVal() allows users to specify the branching point for a variable in contrast to SCIPbranchVar(), which will always use the current LP or pseudo solution. This paragraph contains additional information regarding how the method SCIPbranchVarVal() works. For external branching candidates, there are three principle possibilities:
See the BRANCHEXECEXT callback in src/scip/branch_random.c for an example. In addition, if a proven lower bound of a created child node is known the user may call the method SCIPupdateNodeLowerbound() in order to update the child node's lower bound. Please also see the further information for the three execution methods. BRANCHEXECPSThe BRANCHEXECPS callback is executed during node processing if no LP solution is available and at least one of the integer variables is not yet fixed. It should split the current problem into smaller subproblems. PS stands for pseudo solution which is the vector of all variables set to their locally best (w.r.t. the objective function) bounds. The user gains access to the branching candidates, i.e., to the non-fixed integer variables, by calling the method SCIPgetPseudoBranchCands(). Furthermore, SCIP provides two methods for performing the actual branching, namely SCIPbranchVar() and SCIPcreateChild(). Given an integer variable
See the BRANCHEXECPS callback in src/scip/branch_random.c for an example. In addition, if a proven lower bound of a created child node is known, the user may call the method SCIPupdateNodeLowerbound() in order to update the child node's lower bound. Please also see the further information for the three execution methods. Further information for the three execution methodsIn order to apply more general branching schemes, one should use the method SCIPcreateChild(). After having created a child node, the additional restrictions of the child node have to be added with calls to SCIPaddConsNode(), SCIPchgVarLbNode(), or SCIPchgVarUbNode(). In some cases, the branching rule can tighten the current subproblem instead of producing a branching. For example, strong branching might have proven that rounding up a variable would lead to an infeasible LP relaxation and thus, the variable must be rounded down. Therefore, the BRANCHEXECLP, BRANCHEXECPS and BRANCHEXECREL callbacks may also produce domain reductions or add additional constraints to the current subproblem. The execution callbacks have the following options:
Only the BRANCHEXECLP callback has the possibility to add a cutting plane to the LP (result SCIP_SEPARATED). BRANCHFREEIf you are using branching rule data, you have to implement this method in order to free the branching rule data. This can be done by the following procedure: static
SCIP_DECL_BRANCHFREE(branchFreeMybranchingrule)
{
SCIP_BRANCHRULEDATA* branchruledata;
branchruledata = SCIPbranchruleGetData(branchrule);
assert(branchruledata != NULL);
SCIPfreeMemory(scip, &branchruledata);
SCIPbranchruleSetData(branchrule, NULL);
return SCIP_OKAY;
}
If you have allocated memory for fields in your branching rule data, remember to free this memory before freeing the branching rule data itself. If you are using the C++ wrapper class, this method is not available. Instead, just use the destructor of your class to free the member variables of your class. BRANCHINITThe BRANCHINIT callback is executed after the problem is transformed. The branching rule may, e.g., use this call to initialize its branching rule data. BRANCHCOPYThe BRANCHCOPY callback is executed when a SCIP instance is copied, e.g. to solve a sub-SCIP. By defining this callback as BRANCHEXITThe BRANCHEXIT callback is executed before the transformed problem is freed. In this method, the branching rule should free all resources that have been allocated for the solving process in BRANCHINIT. BRANCHINITSOLThe BRANCHINITSOL callback is executed when the presolving is finished and the branch-and-bound process is about to begin. The branching rule may use this call to initialize its branch-and-bound specific data. BRANCHEXITSOLThe BRANCHEXITSOL callback is executed before the branch-and-bound process is freed. The branching rule should use this call to clean up its branch-and-bound data. |



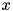 with fractional LP solution value
with fractional LP solution value 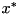 , the method
, the method 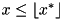 and the other one contains the bound
and the other one contains the bound 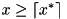 , see the BRANCHEXECLP callback in
, see the BRANCHEXECLP callback in 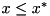 and the other one contains the bound
and the other one contains the bound  .
.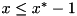 , one contains the bound
, one contains the bound 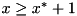 , one contains the fixing
, one contains the fixing 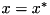 .
.![$[l,u]$](form_30.png) and not having solved the LP, the method
and not having solved the LP, the method 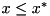 , and
, and 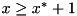 with
with 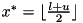 . The current pseudo solution will remain feasible in one of the branches, but the hope is that halving the domain's size leads to good propagations.
. The current pseudo solution will remain feasible in one of the branches, but the hope is that halving the domain's size leads to good propagations.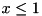 ,
, 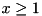 , and
, and 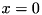 .
.