Feasible solutions can be found in two different ways during the traversal of the branch-and-bound tree. On one hand, the solution of a node's relaxation may be feasible with respect to the constraints (including the integrality). On the other hand, feasible solutions can be discovered by primal heuristics.
A complete list of all primal heuristics contained in this release can be found here.
We now explain how users can add their own primal heuristics. Take the simple and fast LP rounding heuristic (src/scip/heur_simplerounding.c) as an example. The idea of simple rounding is to iterate over all fractional variables of an LP solution and round them down, if the variables appears only with nonnegative coefficients in the system Ax <= b and round them up if the variables appears only with nonpositive coefficients. If one of both conditions applies for each of the fractional variables, this will give a feasible solution. As all other default plugins, it is written in C. C++ users can easily adapt the code by using the scip::ObjHeur wrapper base class and implement the scip_...() virtual methods instead of the SCIP_DECL_HEUR... callback methods.
Additional documentation for the callback methods of a primal heuristic can be found in the file type_heur.h.
Here is what you have to do to implement a primal heuristic:
- Copy the template files src/scip/heur_xyz.c and src/scip/heur_xyz.h into files named "heur_myheuristic.c" and "heur_myheuristic.h".
Make sure to adjust your Makefile such that these files are compiled and linked to your project.
- Use SCIPincludeHeurMyheuristic() in order to include the heuristic into your SCIP instance, e.g., in the main file of your project (see, e.g., src/main.c in the Coloring example).
- Open the new files with a text editor and replace all occurrences of "xyz" by "myheuristic".
- Adjust the properties of the primal heuristic (see Properties of a Primal Heuristic).
- Define the primal heuristic data (see Primal Heuristic Data). This is optional.
- Implement the interface methods (see Interface Methods).
- Implement the fundamental callback methods (see Fundamental Callback Methods of a Primal Heuristic).
- Implement the additional callback methods (see Additional Callback Methods of a Primal Heuristic). This is optional.
Properties of a Primal Heuristic
At the top of the new file "heur_myheuristic.c" you can find the primal heuristic properties. These are given as compiler defines. In the C++ wrapper class, you have to provide the primal heuristic properties by calling the constructor of the abstract base class scip::ObjHeur from within your constructor. Of course, all of them are of relevant, but the most important ones for controlling the performance are usually HEUR_FREQ and HEUR_TIMING. The properties you have to set have the following meaning:
- HEUR_NAME: the name of the primal heuristic.
- This name is used in the interactive shell to address the primal heuristic. Additionally, if you are searching for a primal heuristic with SCIPfindHeur(), this name is looked up. Names have to be unique: no two primal heuristics may have the same name.
- HEUR_DESC: the description of the primal heuristic.
- This string is printed as a description of the primal heuristic in the interactive shell when you call "display heuristics".
- HEUR_DISPCHAR: the display character of the primal heuristic.
- In the interactive shell, this character is printed in the first column of a status information row, if the primal heuristic found the feasible solution belonging to the primal bound. Note that a star '*' stands for an integral LP-relaxation. In order to avoid confusion, display characters should be unique: no two primal heuristics should have the same display character. You can get a list of all primal heuristics along with their display characters by entering "display heuristics" in the SCIP interactive shell.
- HEUR_PRIORITY: the priority of the primal heuristic.
- At each of the different entry points of the primal heuristics during the solving process (see HEUR_TIMING), they are called in decreasing order of their priority.
The priority of a primal heuristic should be set according to the complexity of the heuristic and the likelihood to find feasible solutions: primal heuristics that provide fast algorithms that often succeed in finding a feasible solution should have a high priority (like simple rounding). In addition, the interaction between different types of primal heuristics should be taken into account. For example, improvement heuristics, which try to generate improved solutions by inspecting one or more of the feasible solutions that have already been found, should have a low priority (like Crossover which by default needs at least 3 feasible solutions).
- HEUR_FREQ: the default frequency for executing the primal heuristic.
- The frequency together with the frequency offset (see HEUR_FREQOFS) defines the depth levels at which the execution method of the primal heuristic HEUREXEC is called. For example, a frequency of 7 together with a frequency offset of 5 means, that the HEUREXEC callback is executed for subproblems that are in depth 5, 12, 19, ... of the branching tree. A frequency of 0 together with a frequency offset of 3 means, that the execution method is only called at those nodes that are in depth level 3 (i.e., at most for
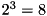 nodes if binary branching is applied). Typical cases are: A frequency of 0 and an offset of 0 which means that the heuristic is only called at the root node and a frequency of -1 which disables the heuristic.
nodes if binary branching is applied). Typical cases are: A frequency of 0 and an offset of 0 which means that the heuristic is only called at the root node and a frequency of -1 which disables the heuristic.
The frequency can be adjusted by the user. This property of the primal heuristic only defines the default value of the frequency. If you want to have a more flexible control of when to execute the primal heuristic, you have to assign a frequency of 1 and implement a check at the beginning of your execution method whether you really want to search for feasible solutions or not. If you do not want to execute the method, set the result code to SCIP_DIDNOTRUN.
- HEUR_FREQOFS: the frequency offset for executing the primal heuristic.
- The frequency offset defines the depth of the branching tree at which the primal heuristic is executed for the first time. For example, a frequency of 7 (see HEUR_FREQ) together with a frequency offset of 10 means, that the callback is executed for subproblems that are in depth 10, 17, 24, ... of the branching tree. In particular, assigning different offset values to heuristics of the same type, like diving heuristics, can be useful for evenly spreading the application of these heuristics across the branch-and-bound tree. Note that if the frequency is equal to 1, the heuristic is applied for all nodes with depth level larger or equal to the frequency offset.
- HEUR_MAXDEPTH: the maximal depth level for executing the primal heuristic.
- This parameter denotes the maximal depth level in the branching tree up to which the execution method of the primal heuristic is called. Use -1 for no limit (a usual case).
- HEUR_TIMING: the execution timing of the primal heuristic.
- Primal heuristics have different entry points during the solving process and the execution timing parameter defines the entry point at which the primal heuristic is executed first.
The primal heuristic can be called first:
- before the processing of the node starts (SCIP_HEURTIMING_BEFORENODE)
- after each LP solve during the cut-and-price loop (SCIP_HEURTIMING_DURINGLPLOOP)
- after the cut-and-price loop was finished (SCIP_HEURTIMING_AFTERLPLOOP)
- after the processing of a node with solved LP was finished (SCIP_HEURTIMING_AFTERLPNODE)
- after the processing of a node without solved LP was finished (SCIP_HEURTIMING_AFTERPSEUDONODE)
- after the processing of the last node in the current plunge was finished, and only if the LP was solved for this node (SCIP_HEURTIMING_AFTERLPPLUNGE)
- after the processing of the last node in the current plunge was finished, and only if the LP was not solved for this node (SCIP_HEURTIMING_AFTERPSEUDOPLUNGE).
- A plunge is the successive solving of child and sibling nodes in the search tree. The flags listed above can be combined to call the heuristic at multiple times by concatenating them with a bitwise OR. Two useful combinations are already predefined:
- after the processing of a node was finished (SCIP_HEURTIMING_AFTERNODE; combines SCIP_HEURTIMING_AFTERLPNODE and SCIP_HEURTIMING_AFTERPSEUDONODE)
- after the processing of the last node in the current plunge was finished (SCIP_HEURTIMING_AFTERPLUNGE; combines SCIP_HEURTIMING_AFTERLPPLUNGE and SCIP_HEURTIMING_AFTERPSEUDOPLUNGE)
- Calling a primal heuristic "before the processing of the node starts" is particularly useful for heuristics that do not need to access the LP solution of the current node. If such a heuristic finds a feasible solution, the leaves of the branching tree exceeding the new primal bound are pruned. It may happen that even the current node can be cut off without solving the LP relaxation. Combinatorial heuristics, like the farthest insert heuristic for the TSP (see examples/TSP/src/HeurFarthestInsert.cpp), are often applicable at this point.
Very fast primal heuristics that require an LP solution can also be called "after each LP solve during the
cut-and-price loop". Rounding heuristics, like the simple and fast LP rounding heuristic (src/scip/heur_simplerounding.c), belong to this group of primal heuristics.
Most heuristics, however, are called either after a node was completely processed (e.g. expensive rounding heuristics like RENS), or even only after a full plunge was finished (e.g., diving heuristics).
- HEUR_USESSUBSCIP: Does the heuristic use a secondary SCIP instance?
- Some heuristics and separators solve MIPs or SAT problems using a secondary SCIP instance. Examples are Large Neighborhood Search heuristics such as RINS and Local Branching or the CGMIP separator. To avoid recursion, these plugins usually deactivate all other plugins that solve MIPs. If a heuristic uses a secondary SCIP instance, this parameter has to be TRUE and it is recommended to call SCIPsetSubscipsOff() for the secondary SCIP instance.
Computational experiments indicate that for the overall performance of a MIP solver, it is important to evenly spread the application of the heuristics across the branch-and-bound tree. Thus, the assignment of the parameters HEUR_FREQ, HEUR_FREQOFS, and HEUR_TIMING should contribute to this aim.
Note that all diving heuristics in the SCIP distribution (see, e.g., src/scip/heur_guideddiving.c) check whether other diving heuristics have already been called at the current node. This can be done by comparing SCIPgetLastDivenode(scip) and SCIPgetNNodes(scip). If the two are equal, and if the current node is not the root node (SCIPgetDepth(scip) > 0), diving heuristics should be delayed by returning the result code 'SCIP_DELAYED'. This is an additional contribution to the goal of not calling multiple similar heuristics at the same node.
Primal Heuristic Data
Below the header "Data structures" you can find a struct which is called "struct SCIP_HeurData". In this data structure, you can store the data of your primal heuristic. For example, you should store the adjustable parameters of the primal heuristic or a working solution in this data structure. If you are using C++, you can add primal heuristic data as usual as object variables to your class.
Defining primal heuristic data is optional. You can leave the struct empty.
Interface Methods
At the bottom of "heur_myheuristic.c", you can find the interface method SCIPincludeHeurMyheuristic(), which also appears in "heur_myheuristic.h" SCIPincludeHeurMyheuristic() is called by the user, if (s)he wants to include the heuristic, i.e., if (s)he wants to use the heuristic in his/her application.
This method only has to be adjusted slightly. It is responsible for notifying SCIP of the presence of the heuristic. For this, you can either call SCIPincludeHeur(), or SCIPincludeHeurBasic() since SCIP version 3.0. In the latter variant, additional callbacks must be added via setter functions as, e.g., SCIPsetHeurCopy(). We recommend this latter variant because it is more stable towards future SCIP versions which might have more callbacks, whereas source code using the first variant must be manually adjusted with every SCIP release containing new callbacks for heuristics in order to compile.
If you are using primal heuristic data, you have to allocate the memory for the data at this point. You can do this by calling:
You also have to initialize the fields in struct SCIP_HeurData afterwards.
You may also add user parameters for your primal heuristic, see the method SCIPincludeHeurFeaspump() in src/scip/heur_oneopt.c for an example where a single Boolean parameter is added.
Fundamental Callback Methods of a Primal Heuristic
The fundamental callback methods of the plugins are the ones that have to be implemented in order to obtain an operational algorithm. They are passed together with the primal heuristic itself to SCIP using SCIPincludeHeur() or SCIPincludeHeurBasic(), see Interface Methods.
Primal heuristic plugins have only one fundamental callback method, namely the HEUREXEC method. This method has to be implemented for every primal heuristic; the other callback methods are optional. In the C++ wrapper class scip::ObjHeur, the scip_exec() method (which corresponds to the HEUREXEC callback) is a virtual abstract member function. You have to implement it in order to be able to construct an object of your primal heuristic class.
Additional documentation for the callback methods can be found in type_heur.h.
HEUREXEC
The HEUREXEC callback is called at different positions during the node processing loop, see HEUR_TIMING. It should search for feasible solutions and add them to the solution pool. For creating a new feasible solution, the methods SCIPcreateSol() and SCIPsetSolVal() can be used. Afterwards, the solution can be added to the storage by calling the method SCIPtrySolFree() (or SCIPtrySol() and SCIPfreeSol()).
The HEUREXEC callback gets a SCIP pointer, a pointer to the heuristic itself, the current point in the solve loop and a result pointer as input (see type_heur.h).
The heuristic has to set the result pointer appropriately! Therefore it has the following options:
- finding at least one feasible solution (result SCIP_FOUNDSOL)
- stating that the primal heuristic searched, but did not find a feasible solution (result SCIP_DIDNOTFIND)
- stating that the primal heuristic was skipped (result SCIP_DIDNOTRUN)
- stating that the primal heuristic was skipped, but should be called again (result SCIP_DELAYED).
Additional Callback Methods of a Primal Heuristic
The additional callback methods do not need to be implemented in every case. However, some of them have to be implemented for most applications, they can be used, for example, to initialize and free private data. Additional callbacks can either be passed directly with SCIPincludeHeur() to SCIP or via specific setter functions after a call of SCIPincludeHeurBasic(), see also Interface Methods.
HEURFREE
If you are using primal heuristic data, you have to implement this method in order to free the primal heuristic data. This can be done by the following procedure:
static
{
assert(heurdata !=
NULL);
}
If you have allocated memory for fields in your primal heuristic data, remember to free this memory before freeing the primal heuristic data itself. If you are using the C++ wrapper class, this method is not available. Instead, just use the destructor of your class to free the member variables of your class.
HEURINIT
The HEURINIT callback is executed after the problem is transformed. The primal heuristic may, e.g., use this call to initialize its primal heuristic data.
HEURCOPY
The HEURCOPY callback is executed when a SCIP instance is copied, e.g. to solve a sub-SCIP. By defining this callback as NULL the user disables the execution of the specified heuristic for all copied SCIP instances. This may deteriorate the performance of primal heuristics using sub-SCIPs.
HEUREXIT
The HEUREXIT callback is executed before the transformed problem is freed. In this method, the primal heuristic should free all resources that have been allocated for the solving process in HEURINIT.
HEURINITSOL
The HEURINITSOL callback is executed when the presolving is finished and the branch-and-bound process is about to begin. The primal heuristic may use this call to initialize its branch-and-bound specific data.
HEUREXITSOL
The HEUREXITSOL callback is executed before the branch-and-bound process is freed. The primal heuristic should use this call to clean up its branch-and-bound data, which was allocated in HEURINITSOL.



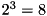 nodes if binary branching is applied). Typical cases are: A frequency of 0 and an offset of 0 which means that the heuristic is only called at the root node and a frequency of -1 which disables the heuristic.
nodes if binary branching is applied). Typical cases are: A frequency of 0 and an offset of 0 which means that the heuristic is only called at the root node and a frequency of -1 which disables the heuristic.