|
All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros Groups Pages
sepa_eccuts.h File Reference Detailed Descriptionedge concave cut separator We call Since the convex envelope of an edge-concave function is a polytope, the value of the convex envelope for a
where We use this as follows: We transform the problem to the unit box For a given quadratic constraint
where each
We solve auxiliary MIP problems to identify good edge-concave aggregations. From the literature it is known that the convex envelope of an bilinear edge-concave function Definition in file sepa_eccuts.h. #include "scip/scip.h"Go to the source code of this file.
Function Documentation
creates the edge-concave separator and includes it in SCIP
|
|||||||||||||||



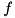 an edge-concave function on a polyhedron
an edge-concave function on a polyhedron 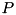 iff it is concave in all edge directions of
iff it is concave in all edge directions of ![$ P = [\ell,u]$](form_203.png) this is equivalent to
this is equivalent to 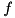 being concave componentwise.
being concave componentwise.![$ x \in [\ell,u] $](form_205.png) can be obtained by solving the following LP:
can be obtained by solving the following LP:![\[ \min \, \sum_i \lambda_i f(v_i) \]](form_206.png)
![\[ s.t. \; \sum_i \lambda_i v_i = x \]](form_207.png)
![\[ \sum_i \lambda_i = 1 \]](form_208.png)
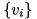 are the vertices of the domain
are the vertices of the domain ![$ [\ell,u] $](form_210.png) . Let
. Let 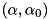 be the dual solution of this LP. It can be shown that
be the dual solution of this LP. It can be shown that 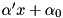 is a facet of the convex envelope of
is a facet of the convex envelope of 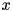 is in the interior of
is in the interior of ![$ [0,1]^n $](form_214.png) by using an linear affine transformation
by using an linear affine transformation 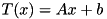 and perturb
and perturb 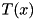 if it is not an interior point. This has the advantage that we do not have to update the matrix of the LP for different edge-concave functions.
if it is not an interior point. This has the advantage that we do not have to update the matrix of the LP for different edge-concave functions.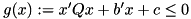 we decompose
we decompose 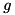 into several edge-concave aggregations and a remaining part, e.g.,
into several edge-concave aggregations and a remaining part, e.g.,![\[ g(x) = \sum_{i = 1}^k f_i(x) + r(x) \]](form_219.png)
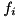 is edge-concave. To separate a given solution
is edge-concave. To separate a given solution 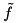 for each edge-concave function
for each edge-concave function 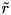 for
for 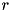 . The resulting cut looks like:
. The resulting cut looks like:![\[ \tilde f_i(x) + \tilde r(x) \le 0 \]](form_224.png)
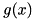 with the previous property using a model based on binary flow arc variables.
with the previous property using a model based on binary flow arc variables.