|
sepa_oddcycle.c File Reference Detailed Descriptionoddcycle separator We separate odd cycle inequalities in the implication graph. Implemented are the classic method by Groetschel, Lovasz, and Schrijver (GLS) and the levelgraph method by Hoffman and Padberg (HP) Odd cycle inequalities are lifted by a heuristic method based on an idea from Alvarez-Valdes, Parreno, and Tamarit. Some part of this code is based on the odd cycle separator of the program colorbitopt by Marc Pfetsch. Definition in file sepa_oddcycle.c. #include <assert.h>#include <string.h>#include "scip/sepa_oddcycle.h"#include "scip/pub_misc.h"#include "dijkstra/dijkstra.h"Go to the source code of this file.
Macro Definition Documentation
Definition at line 41 of file sepa_oddcycle.c. Referenced by SCIP_DECL_SEPACOPY(), and SCIPincludeSepaOddcycle().
Definition at line 42 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
Definition at line 43 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
Definition at line 44 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
Definition at line 45 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
does the separator use a secondary SCIP instance? Definition at line 46 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
should separation method be delayed, if other separators found cuts? Definition at line 47 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
factor for scaling of the arc-weights in the Dijkstra algorithm Definition at line 51 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
use GLS method, otherwise HP method Definition at line 52 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
lift odd cycle cuts Definition at line 53 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
try to repair violated cycles in which a variable and its negated appear Definition at line 54 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
add links between a variable and its negated Definition at line 55 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
separate triangles (3-cliques) found as 3-cycles or repaired larger cycles Definition at line 56 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
still try variable as start, even if it is already covered by a cut Definition at line 57 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
allow another inequality to use variable, even if it is already covered Definition at line 58 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
TRUE: choose lifting candidate with highest value of coefficient*lpvalue FALSE: choose lifting candidate with highest coefficient Definition at line 59 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
whether lifting coefficients should be recomputed Definition at line 62 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of oddcycle cuts separated per separation round Definition at line 63 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of oddcycle cuts separated per separation round in root node Definition at line 64 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
percent of variables to try the chosen method on [0-100] Definition at line 65 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
offset of variables to try the chosen method on Definition at line 66 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of oddcycle cuts generated per root of the levelgraph Definition at line 67 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
unsorted (0), maxlp (1), minlp (2), maxfrac (3), minfrac (4) Definition at line 68 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
minimal weight on an edge (in level graph or Dijkstra graph) Definition at line 69 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of rounds pre node Definition at line 70 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of rounds in the root node Definition at line 71 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of levels in level graph Definition at line 72 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal percentage of nodes allowed in one level of the levelgraph [0-100] Definition at line 73 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
additional offset of nodes allowed in one level of the levelgraph Definition at line 74 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
sort neighbors of the root in the level graph Definition at line 75 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of cuts produced per level Definition at line 76 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of unsuccessful calls at each node Definition at line 77 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle().
maximal number of other cuts s.t. separation is applied (-1 for direct call) Definition at line 78 of file sepa_oddcycle.c. Referenced by SCIPincludeSepaOddcycle(). Typedef Documentation
Definition at line 125 of file sepa_oddcycle.c. Definition at line 143 of file sepa_oddcycle.c. Enumeration Type Documentation
sorting type for starting node or root node iteration order If the array should be sorted (1-4), the variable array is sorted every round by the chosen sorttype and the search method tries the nodes in order of the array. If the array is used unsorted (0), the search methods tries the nodes in order of the array and stores the last processed start node or root node and continues from this position in the next separation round. Definition at line 135 of file sepa_oddcycle.c. Function Documentation
using the level graph (if possible) or Dijkstra graph data structure (depending on the used method) we determine whether two nodes are adjacent
Definition at line 269 of file sepa_oddcycle.c. References checkBlocking(), FALSE, NULL, SCIP_Bool, SCIPcliqueGetNVars(), SCIPcliqueGetValues(), SCIPcliqueGetVars(), SCIPvarGetCliques(), SCIPvarGetNCliques(), SCIPvarGetProbindex(), and TRUE. Referenced by checkBlocking(), and getCoef().
inside the lifting heuristic we determine the lifting coefficient by counting the length of chains adjacent to the lifting candidate. since we have to exclude all chains adjacent to an already lifted node which is not adjacent to the current lifting candidate we check all chains of the cycle of length three and block them if they are adjacent.
Definition at line 479 of file sepa_oddcycle.c. References FALSE, getCoef(), isNeighbor(), and NULL. Referenced by getCoef(), and isNeighbor().
determine the heuristic lifting coefficient by counting the length of the adjacent chains of the candidate (we have to exclude all chains that are adjacent to an already lifted node which is not adjacent to the current candidate)
Definition at line 532 of file sepa_oddcycle.c. References checkBlocking(), isNeighbor(), liftOddCycleCut(), NULL, and SCIPfloor(). Referenced by checkBlocking(), and liftOddCycleCut().
Lifting Heuristic based on an idea by Alvarez-Valdes, Parreno, Tamarit This method is based on the observation, that a non-cycle node can be lifted into the inequality with coefficient The coefficient can be calculated as If the node is connected to several chains, the coefficients of the chains can be summed up, resulting in a feasible lifting coefficient. Additionally further variables can be lifted by considering chains connected to the additional lifting node which are not connected to already lifted nodes. This method is a feasible heuristic which gives a valid lifted inequality. (Furthermore the first lifting coefficient is always smaller or equal to the largest possible lifting coefficient.)
Definition at line 668 of file sepa_oddcycle.c. References FALSE, generateOddCycleCut(), getCoef(), NULL, SCIP_Bool, SCIP_CALL, SCIP_OKAY, SCIPallocBufferArray, SCIPfreeBufferArray, SCIPisStopped(), and TRUE. Referenced by generateOddCycleCut(), and getCoef().
add the inequality corresponding to the given odd cycle to the LP (if violated) after lifting it (if requested by user flag)
Definition at line 839 of file sepa_oddcycle.c. References cleanCycle(), FALSE, liftOddCycleCut(), NULL, SCIP_Bool, SCIP_CALL, SCIP_CUTOFF, SCIP_DIDNOTFIND, SCIP_MAXSTRLEN, SCIP_OKAY, SCIP_Real, SCIP_REDUCEDDOM, SCIP_SEPARATED, SCIPaddCut(), SCIPaddPoolCut(), SCIPaddVarToRow(), SCIPallocBufferArray, SCIPcacheRowExtensions(), SCIPchgRowRhs(), SCIPchgVarLb(), SCIPchgVarUb(), SCIPcreateEmptyRowSepa(), SCIPdebugMessage, SCIPflushRowExtensions(), SCIPfreeBufferArray, SCIPinfinity(), SCIPisCutEfficacious(), SCIPisStopped(), SCIPprintRow(), SCIPreleaseRow(), SCIProwChgRank(), SCIProwGetRhs(), SCIPsnprintf(), and TRUE. Referenced by liftOddCycleCut(), separateGLS(), and separateHeur().
check whether the given object is really a cycle without sub-cycles (sub-cycles may be calculated by the GLS algorithm in case there is no violated odd cycle inequality) and removes pairs of original and negated variables from the cycle
Definition at line 1038 of file sepa_oddcycle.c. References checkArraySizesHeur(), FALSE, NULL, SCIP_CALL, SCIP_OKAY, SCIPallocBufferArray, SCIPfreeBufferArray, and TRUE. Referenced by generateOddCycleCut(), separateGLS(), and separateHeur().
memory reallocation method (the graph is normally very dense, so we dynamically allocate only the memory we need) Since the array sizes differ the method can be called for each of the three data structure types:
Definition at line 1206 of file sepa_oddcycle.c. References addArc(), FALSE, MIN, NULL, SCIP_CALL, SCIP_OKAY, SCIP_Real, SCIPdebugMessage, SCIPgetMemExternEstim(), SCIPgetMemUsed(), SCIPgetRealParam(), SCIPisInfinity(), SCIPisStopped(), and SCIPreallocBufferArray. Referenced by addArc(), cleanCycle(), createNextLevel(), and insertSortedRootNeighbors().
Add arc to level graph
Definition at line 1291 of file sepa_oddcycle.c. References addNextLevelCliques(), checkArraySizesHeur(), NULL, SCIP_CALL, and SCIP_OKAY. Referenced by addNextLevelCliques(), checkArraySizesHeur(), and createNextLevel().
add implications from cliques of the given node u
Definition at line 1368 of file sepa_oddcycle.c. References addArc(), FALSE, insertSortedRootNeighbors(), MAX, NULL, SCIP_Bool, SCIP_CALL, SCIP_OKAY, SCIPcliqueGetNVars(), SCIPcliqueGetValues(), SCIPcliqueGetVars(), SCIPfeasCeil(), SCIPisFeasIntegral(), SCIPvarGetCliques(), SCIPvarGetNCliques(), SCIPvarGetProbindex(), and TRUE. Referenced by addArc(), and createNextLevel().
sort level of root neighbors If we limit the size of nodes of a level, we want to add the best neighbors to the next level. Since sorting every level is too expensive, we sort the neighbors of the root (if requested). Create the first level as follows:
Even inserting all variables might help for the following creation of further levels since the neighbors of nodes with high fractionality often have high fractionalities themselves and would be inserted first when further levels would have been sorted (which actually is not the case).
Definition at line 1533 of file sepa_oddcycle.c. References BMSclearMemoryArray, checkArraySizesHeur(), FALSE, findShortestPathToRoot(), MAX, MIN, NULL, SCIP_Bool, SCIP_CALL, SCIP_OKAY, SCIP_Real, SCIPallocBufferArray, SCIPcliqueGetNVars(), SCIPcliqueGetValues(), SCIPcliqueGetVars(), SCIPfeasCeil(), SCIPfreeBufferArray, SCIPisFeasIntegral(), SCIPsortDownRealInt(), SCIPvarGetCliques(), SCIPvarGetNCliques(), SCIPvarGetProbindex(), and TRUE. Referenced by addNextLevelCliques(), and createNextLevel().
Find shortest path from start node to root We perform a BFS to find the shortest path to the root. D stores the distance to the start node, P stores the partent nodes in the shortest path tree (-1 if node has not been reached).
Definition at line 1736 of file sepa_oddcycle.c. References blockRootPath(), FALSE, NULL, SCIP_OKAY, and TRUE. Referenced by insertSortedRootNeighbors(), and separateHeur().
Block shortest path We traverse the shortest path found by findShortestPathToRoot() and block all neighbors (in the original graph) of nodes in the path, i.e., we set blocked to TRUE. We do not block neighbors of the root node, since they have to be used. For the start node we only block nodes on the previous layers,
Definition at line 1827 of file sepa_oddcycle.c. References findUnblockedShortestPathToRoot(), NULL, SCIP_OKAY, and TRUE. Referenced by findShortestPathToRoot(), and separateHeur().
Find shortest path from root to target node We perform a BFS to find the shortest path from the root. The only difference to findShortestPathToRoot() is that we avoid nodes that are blocked.
Definition at line 1916 of file sepa_oddcycle.c. References createNextLevel(), FALSE, NULL, SCIP_CALL, SCIP_OKAY, SCIPallocBufferArray, SCIPfreeBufferArray, and TRUE. Referenced by blockRootPath(), and separateHeur().
create next level of level graph for odd cycle separation
Definition at line 2036 of file sepa_oddcycle.c. References addArc(), addNextLevelCliques(), checkArraySizesHeur(), insertSortedRootNeighbors(), NULL, SCIP_CALL, SCIP_OKAY, separateHeur(), and TRUE. Referenced by findUnblockedShortestPathToRoot(), and separateHeur().
The heuristic method for finding odd cycles by Hoffman, Padberg uses a level graph which is constructed as follows: First we choose a node (i.e. a variable of the problem or its negated) as root and assign it to level 0 (and no other node is assigned to level 0). All neighbors of the root are assigned to level 1 and the arcs between are added. In general: All neighbors of nodes in level i that are assigned to level i+1, if they do not already appear in levels <= i. All arcs between nodes in level i and their neighbors are added. In the construction we only take nodes that are contained in the fractional graph, i.e., their current LP values are not integral. Since SCIP stores implications between original and negated variables, the level graph has at most twice the number of fractional binary variables of the problem. Since the implication graph of SCIP is (normally) incomplete, it is possible to use arcs between an original variable and its negated to obtain more cycles which are valid but not found due to missing links.
Definition at line 2213 of file sepa_oddcycle.c. References blockRootPath(), BMSclearMemoryArray, checkArraySizesGLS(), cleanCycle(), createNextLevel(), DIJKSTRA_UNUSED, FALSE, findShortestPathToRoot(), findUnblockedShortestPathToRoot(), generateOddCycleCut(), MAXIMAL_FRACTIONALITY, MAXIMAL_LPVALUE, MIN, MINIMAL_FRACTIONALITY, MINIMAL_LPVALUE, NULL, SCIP_Bool, SCIP_CALL, SCIP_CUTOFF, SCIP_INVALIDDATA, SCIP_OKAY, SCIP_Real, SCIP_VARTYPE_CONTINUOUS, SCIPABORT, SCIPallocBufferArray, SCIPceil(), SCIPerrorMessage, SCIPfreeBufferArray, SCIPgetSolVal(), SCIPgetVarsData(), SCIPisFeasIntegral(), SCIPisStopped(), SCIPsortDownRealPtr(), SCIPsortRealPtr(), SCIPvarGetNCliques(), SCIPvarGetProbindex(), SCIPvarGetType(), SCIPvarIsBinary(), TRUE, and UNSORTED. Referenced by createNextLevel(), and SCIP_DECL_SEPAEXECLP().
memory reallocation method (the graph is normally very dense, so we dynamically allocate only the memory we need)
Definition at line 2701 of file sepa_oddcycle.c. References addGLSCliques(), DIJKSTRA_UNUSED, FALSE, DIJKSTRA_Graph::head, MIN, NULL, SCIP_CALL, SCIP_OKAY, SCIP_Real, SCIPdebugMessage, SCIPgetMemExternEstim(), SCIPgetMemUsed(), SCIPgetRealParam(), SCIPisInfinity(), SCIPisStopped(), SCIPreallocBufferArray, and DIJKSTRA_Graph::weight. Referenced by addGLSCliques(), separateGLS(), and separateHeur().
add implications from cliques of the given node
Definition at line 2779 of file sepa_oddcycle.c. References checkArraySizesGLS(), FALSE, DIJKSTRA_Graph::head, MAX, DIJKSTRA_Graph::maxweight, DIJKSTRA_Graph::minweight, NULL, DIJKSTRA_Graph::outcnt, SCIP_Bool, SCIP_CALL, SCIP_OKAY, SCIPcliqueGetNVars(), SCIPcliqueGetValues(), SCIPcliqueGetVars(), SCIPfeasCeil(), SCIPisFeasIntegral(), SCIPvarGetCliques(), SCIPvarGetProbindex(), separateGLS(), and DIJKSTRA_Graph::weight. Referenced by checkArraySizesGLS(), and separateGLS().
The classical method for finding odd cycles by Groetschel, Lovasz, Schrijver uses a bipartite graph which contains in each partition a node for every node in the original graph. All arcs uv of the original graph are copied to arcs from u of the first partition to v' of the second partition and from u' of the second partition to v of the first partition. A Dijkstra algorithm is used to find a path from a node x to its copy x', if existing. The nodes in the original graph corresponding to the nodes on the path form an odd cycle. Since SCIP stores implications between original and negated variables, our original graph has at most twice the number of binary variables of the problem. By creating the bipartite graph we gain 4 segments of the graph: I - nodes of the original variables in the first bipartition The length of every segment if the number of binary variables in the original problem. Since the implication graph of SCIP is (normally) incomplete, it is possible to use arcs between an original variable and its negated to obtain more cycles which are valid but not found due to missing links.
Definition at line 2938 of file sepa_oddcycle.c. References addGLSCliques(), DIJKSTRA_Graph::arcs, BMSclearMemoryArray, checkArraySizesGLS(), cleanCycle(), DIJKSTRA_FARAWAY, DIJKSTRA_UNUSED, dijkstraGraphIsValid(), dijkstraPairCutoff(), dijkstraPairCutoffIgnore(), FALSE, generateOddCycleCut(), DIJKSTRA_Graph::head, MAXIMAL_FRACTIONALITY, MAXIMAL_LPVALUE, DIJKSTRA_Graph::maxweight, MIN, MINIMAL_FRACTIONALITY, MINIMAL_LPVALUE, DIJKSTRA_Graph::minweight, DIJKSTRA_Graph::nodes, NULL, DIJKSTRA_Graph::outbeg, DIJKSTRA_Graph::outcnt, SCIP_Bool, SCIP_CALL, SCIP_DECL_SEPACOPY(), SCIP_INVALIDDATA, SCIP_MAXSTRLEN, SCIP_OKAY, SCIP_Real, SCIP_VARTYPE_CONTINUOUS, SCIP_VERBLEVEL_HIGH, SCIPABORT, SCIPallocBufferArray, SCIPceil(), SCIPdebugMessage, SCIPerrorMessage, SCIPfreeBufferArray, SCIPgetNLPs(), SCIPgetProbName(), SCIPgetSolVal(), SCIPgetVarsData(), SCIPisFeasIntegral(), SCIPisStopped(), SCIPsnprintf(), SCIPsortDownRealPtr(), SCIPsortRealPtr(), SCIPsplitFilename(), SCIPvarGetNCliques(), SCIPvarGetProbindex(), SCIPvarGetType(), SCIPvarIsBinary(), SCIPverbMessage(), SCIPwriteCliqueGraph(), TRUE, UNSORTED, and DIJKSTRA_Graph::weight. Referenced by addGLSCliques(), and SCIP_DECL_SEPAEXECLP().
copy method for separator plugins (called when SCIP copies plugins) Definition at line 3456 of file sepa_oddcycle.c. References NULL, SCIP_CALL, SCIP_DECL_SEPAFREE(), SCIP_OKAY, SCIPincludeSepaOddcycle(), SCIPsepaGetName(), and SEPA_NAME. Referenced by separateGLS().
destructor of separator to free user data (called when SCIP is exiting) Definition at line 3471 of file sepa_oddcycle.c. References NULL, SCIP_DECL_SEPAINIT(), SCIP_OKAY, SCIPfreeMemory, SCIPsepaGetData(), and SCIPsepaSetData(). Referenced by SCIP_DECL_SEPACOPY().
initialization method of separator (called after problem was transformed) Definition at line 3487 of file sepa_oddcycle.c. References NULL, SCIP_DECL_SEPAINITSOL(), SCIP_OKAY, and SCIPsepaGetData(). Referenced by SCIP_DECL_SEPAFREE().
solving process initialization method of separator (called when branch and bound process is about to begin) Definition at line 3507 of file sepa_oddcycle.c. References NULL, SCIP_DECL_SEPAEXECLP(), SCIP_OKAY, and SCIPsepaGetData(). Referenced by SCIP_DECL_SEPAINIT().
LP solution separation method of separator Definition at line 3525 of file sepa_oddcycle.c. References NULL, SCIP_CALL, SCIP_DIDNOTFIND, SCIP_DIDNOTRUN, SCIP_OKAY, SCIPdebugMessage, SCIPgetCurrentNode(), SCIPgetDepth(), SCIPgetNBinVars(), SCIPgetNCliques(), SCIPgetNCutsFoundRound(), SCIPgetNImplications(), SCIPgetNLPBranchCands(), SCIPincludeSepaOddcycle(), SCIPnodeGetNumber(), SCIPsepaGetData(), SCIPsepaGetNCallsAtNode(), SCIPsepaGetTime(), separateGLS(), and separateHeur(). Referenced by SCIP_DECL_SEPAINITSOL().
creates the oddcycle separator and includes it in SCIP
Definition at line 3629 of file sepa_oddcycle.c. References DEFAULT_ADDSELFARCS, DEFAULT_ALLOWMULTIPLECUTS, DEFAULT_CUTTHRESHOLD, DEFAULT_INCLUDETRIANGLES, DEFAULT_LIFTODDCYCLES, DEFAULT_LPLIFTCOEF, DEFAULT_MAXCUTSLEVEL, DEFAULT_MAXCUTSROOT, DEFAULT_MAXNLEVELS, DEFAULT_MAXPERNODESLEVEL, DEFAULT_MAXREFERENCE, DEFAULT_MAXROUNDS, DEFAULT_MAXROUNDSROOT, DEFAULT_MAXSEPACUTS, DEFAULT_MAXSEPACUTSROOT, DEFAULT_MAXUNSUCESSFULL, DEFAULT_MULTIPLECUTS, DEFAULT_OFFSETNODESLEVEL, DEFAULT_OFFSETTESTVARS, DEFAULT_PERCENTTESTVARS, DEFAULT_RECALCLIFTCOEF, DEFAULT_REPAIRCYCLES, DEFAULT_SCALEFACTOR, DEFAULT_SORTROOTNEIGHBORS, DEFAULT_SORTSWITCH, DEFAULT_USEGLS, FALSE, NULL, SCIP_CALL, SCIP_OKAY, SCIPaddBoolParam(), SCIPaddIntParam(), SCIPallocMemory, SCIPincludeSepaBasic(), SCIPsetSepaCopy(), SCIPsetSepaFree(), SCIPsetSepaInit(), SCIPsetSepaInitsol(), SEPA_DELAY, SEPA_DESC, SEPA_FREQ, SEPA_MAXBOUNDDIST, SEPA_NAME, SEPA_PRIORITY, SEPA_USESSUBSCIP, and TRUE. Referenced by SCIP_DECL_SEPACOPY(), SCIP_DECL_SEPAEXECLP(), and SCIPincludeDefaultPlugins(). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



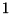 if the node is adjacent to the nodes of a 3-chain on the cycle.
if the node is adjacent to the nodes of a 3-chain on the cycle.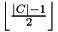 where
where 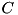 is the chain on the cycle.
is the chain on the cycle.